[논문 리뷰] DDP: Diffusion Model for Dense Visual Prediction

Abstract

• conditional diffusion pipeline에 기초한 dense visual prediction을 위한 framework제시
• noise-to-map; progressively removing noise from a random Gaussian noise, guided by image
• without task-specific design and architecture customization
• Attractive properties: dynamic inference & uncertainty awareness
• Cityscapes val에서 83.9 mIoU (24.07.15 기준 #19)

Introduction

• Dense prediction tasks의 중요성
  • 컴퓨터 비전 연구의 기초로, 의미적 분할, 깊이 추정, 광학 흐름 등을 포함.
  • 이미지에 있는 모든 픽셀에 대한 정확한 예측 요구.
• 기존 방법 두 가지
  1. Discriminative-based: 입력-출력 쌍 사이의 매핑을 배워 단일 전방 단계를 통해 예측. 간단하고 효율적.
  2. Generative-based: 데이터의 기본 분포 모델링, 더 복잡한 작업 처리 능력. 그러나 복잡한 아키텍처 커스터마이제이션 및 다양한 훈련의 어려움 존재.
• Diffusion Model 도입
  • 노이즈를 점진적으로 데이터로 변환하는 과정으로 간단한 훈련 방법 제공.
  • 여러 생성 작업에서 우수한 성능을 발휘.
• DDP 프레임워크
  • Conditional Diffusion Model: 입력 이미지를 기반으로 무작위 가우시안 분포에서 노이즈를 점진적으로 제거하여 결과 예측 생성.
    • Forward Diffusion (𝑞): 데이터에 점진적으로 노이즈 추가.
    • Reverse Diffusion (𝑝𝜃): 노이즈 샘플에서 원하는 예측으로 변환.
    • encoded ground truth + gaussian noise = noisy map
    • noisy map + image features(condition, from image encoder(Swin transformer, ConvNext)) ← concat
    • lightweight map decoder를 사용하여 noise 제거한 prediction 산출
  • image encoder와 map decoder를 분리(decouple)
  • image encoder는 한번만 실행되고, diffusion process는 lightweight decoder head에서만 수행
• DDP의 특
  1. Dinamic inference: 계산과 예측 품질 간의 트레이드오프.
  2. ⇒ 그러면 계산이 늘어날수록 품질이 좋다는거잖아. 근데 step을 늘리면 안좋아지는데?
  3. Uncertainty awareness: 예측의 불확실성을 자연스럽게 인식.
• DDP 성과
  • 여러 데이터셋에서 기존 최고 성능 방법보다 더 나은 결과 도출.
  • 특정 데이터셋에서 선두 결과 도출 예시:
    • ADE20K: 46.1 mIoU
    • nuScenes: 70.3 mIoU
    • Cityscapes: 83.9 mIoU
    • KITTI: 0.05 REL

Related Work

1. Diffusion Model

• Diffusion model과 score-based 생성 모델은 이미지, 비디오, 오디오, 생의학 등 다양한 모달리티에서 뛰어난 결과를 보여줌.
• 이러한 모델을 활용하여 생성 기반의 지각 모델을 개발하면 새로운 수준의 밀집 예측 작업을 달성할 수 있을 것으로 기대됨.

2. Dense Prediction

• dense prediction은 모든 픽셀마다 classification나 regression를 수행하여 장면을 인식하는 것.
• e.g. semantic segmentation, depth estimation, optical flow 등이 있음.
• 높은 성능을 위한 접근법: multi-scale feature aggregation(FPN), high-capacity backbone(Swin Transformer or ConvNext), powerful decoder head(Map decoder) 등이 있음.
• 본 논문에서는 'noise-to-map' 생성 패러다임을 도입.

3.Diffusion Models for Dense Prediction

• 최근 diffusion model이 generation tasks에서 성공을 거두면서, 이를 dense visual prediction tasks에 도입하려는 시도가 증가함.
• 초기 작업 예시:
  • medical image segmentation 분할을 위한 Wolleb et al. [81]
    • Diffusion models for implicit image segmentation ensembles
  • panoptic segmentation을 위한 Pix2Seq-D [14]
    • A generalist framework for panoptic segmentation of images and videos
  • depth estimation을 위한 DepthGen [68]
• 기존 방법들의 한계: parameter-heavy convolution U-Nets를 사용하여 효율성이 낮고 학습이 느리며 최적의 성능 도달이 어려움.
• 제안된 프레임워크: 효과적인 diffusion process을 modern perception pipeline에 통합하였으며, 정확도와 효율성을 유지함.

Methodology

1. Preliminaries

• Dense Prediction
  • The objective: $x \in \mathbb{R}^{3 \times h \times w}$의 모든 pixel에 대해 discrete label 또는 continuous values를 예측하는 것 (denoted $y$)
• Conditional Diffusion Model
  • diffusion model의 확장판, non-equilibrium thermondynamics에서 영감을 받은 likelihood-based models에 속함
  • Forward process
    • $q(z_t | z_0) = N(z_t; \sqrt{\bar{\alpha}_t} z_0, (1 - \bar{\alpha}_t) I)$
      • $q(z_t | z_0)$ : $z_0$에서 $z_t$로의 확률 분포
      • N : normal distribution
      • $\sqrt{\bar{\alpha}_t} z_0$ : 평균
      • $(1 - \bar{\alpha}_t) I$: 공분산 행렬 → 분산
      • $\bar{\alpha}t := \prod{s=0}^{t} \alpha_s = \prod_{s=0}^{t} (1 - \beta_s)$ : 누적 noise schedule
      • $\beta_s$ : 개별 time step의 noise schedule
  • Reverse process : $f_\theta (z_t, x, t)$
    • 조건 $x$의 guide하에 $z_t$에서 $z_0$를 예측하도록 훈련
    • L2 loss를 minimizing ⇒ 하지만 이 논문에서는 L2가 아니라 CE를 사용
    • Inference stage
      • random noise $z_T$에서 $z_0$를 reconstruct
      • markovian way
        • $p_\theta (z_{0:T} | x) = p(z_T) \prod_{t=1}^T p_\theta (z_{t-1} | z_t, x)$
  • In this paper
    • conditional diffusion model을 통해 dense prediction tasks를 해결하는 것이 목표
    • ground truth map $z_0 = y$
    • $f_\theta$는 random noise($z_t \sim \mathcal{N}(0,I$))로부터 $z_0$를 예측하는 neural network
      • input image $x$가 조건으로 들어감

2. Architecture

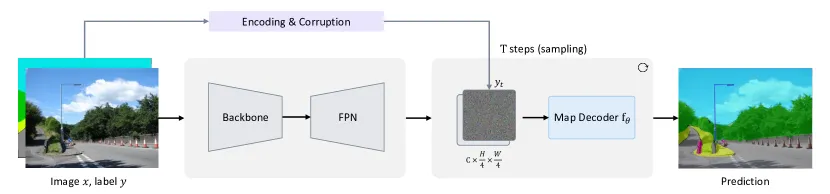
• previous methods: 기존 방식은 여러 단계(multiple steps)에서 모델을 원본 이미지에 적용하여 계산 오버헤드를 크게 증가시킴
• DDP 방식: DDP는 전체 모델을 image encoder와 map decoder로 분리하여 효율성을 높임
  • Image encoder는 input image에서 feature map을 추출, 딱 한번만 실행
  • map decoder: raw image $x$를 condition으로 넣는게 아니라 feature map을 condition으로 넣음. 그리고 gradually refine the prediction ($y_t$ → $y_0$)
• Image encodr
  1. input: 원본 이미지 $𝑥$
  2. output: 서로 다른 4가지 resolution의 multi-scale features 특징을 생성
  3. feature aggregation : multi-scale features을 FPN(Fully-Connected Network) 을 사용해 fusion, 1x1 conv로 aggregation합니다.
  4. final feature map: resolution이  $256 \times \frac{h}{4} \times \frac{w}{4}$인 feature map이 생성되며, 이는 map decoder의 조건으로 사용됨 (조건은 concat)
  5. Backbone: ConvNext와 Swin Transformer 같은 모던 네트워크 아키텍처와 호환 가능 (MedSegDiff, SegDiff 이건 안됐나봄)
• Map Decoder
  1. input: noisy map($y_t$)와 image encoder의 feature map
  2. pixel-level classification 또는 regression를 수행하며, feature map과 noisy map($y_t$)을 concatenation하여 input으로 사용
     • 코드를 보니 concatenation 후 convModule에 넣어주고 이 output을 model에 넣음
  3. Structure: 변형 가능한 어텐션(deformable attention) layer 6개를 쌓아 구성.
  4. 경량화: 기존의 무겁고 매개변수가 많은 U-Net(parameter-intensive U-Net) 대신, lightweight and compact한 구조를 채택. 이를 통해 multi-step reverse diffusion process에서 shared parameters의 효율적인 재사용 가능

3. Training

• Label encoding - ground truth를 encoding하는 것
  • standard diffusion model은 원래 continious data를 가정 → regression에는 적합(depth estimation)
  • 그러나 discrete label에는 부적합(sem. seg.)
  • 그래서 discrete label을 3가지 encoding 전략으로 encoding 수행해봄
    1. One-hot encoding
    2. Analog bits encoding
       1. A generalist framework for panoptic segmentation of images and videos
       2. Analog Bits: Generating Discrete Data using Diffusion Models with Self-Conditioning
       • discrete integer를 bit strings로 변환 후 real number로 cast
    3. Class embedding → 가장 효과적
       • learnable embedding layer를 사용하여 discrete label을 high-dimensional continuous space에 projection후 sigmoid로 normalization
  • 모든 encoding 방법에서 [-scale, +scale]로 정규화 scaling
    • bit_scale = 0.01 확인 (Table 5.b)
    • one-hot에서는 0.1
    • scaling factor는 SNR(signal to noise ratio)를 제어하는 중요한 hyperparameter라고 함
• Map Corruption
  • encoded ground truth에 noise추가하여 noisy map $y_t$ 생성
  • noise 강도는 $a_t$로 조절 (t에 따라 단조증가)
  • cosine schedule vs. linear schedule
• Objective Function
  • Standard diffusion model은 l2 loss를 사용하는데, supervision에서 task-specific loss를 사용하는게 더 낫더라
  • CE - sem. seg., sigloss - depth estimation

4. Inference

• test image가 condition input으로 주어짐(image encoder를 통과)
• Gaussian distribution에서 sampling된 noise map으로 시작
• Sampling Rule:
  • DDIM 업데이트 규칙 사용.
  • 각 샘플링 단계 𝑡에서  $𝑦_𝑇$또는 이전 단계의 예측된 노이즈 맵 $𝑦_{𝑡+1}$를 conditional feature map과 융합(fuse).
  • 이 fused map을 map decoder $𝑓_\theta$에 전달하여 맵 예측.
  • 이후, 현재 단계의 예측 결과를 사용하여 다음 단계의 노이즈 맵($y_t$)계산.
• Sampling Drift (성능 드리프트):
  • 모델 성능은 몇 가지 샘플링 단계에서 개선되다가, 샘플링 단계가 증가함에 따라 약간 감소.
  • 훈련 중에는 노이즈가 추가된 실제 지도를 역으로 복원하도록 학습되지만, 테스트 시에는 모델의 불완전한 예측(imperfect prediction)에서 노이즈를 제거해야 함.
  • 이로 인해, 훈련 데이터와 샘플링 데이터 분포 간에 불일치가 발생.
  • 작은 시간 단계에서 복합된 오류(compounded errors)로 이 drift가 더 두드러짐.
  • 또한, 샘플이 실제 분포에서 벗어날수록 더욱 강화
• Self-Aligned Denoising: Sampling Drift를 이걸로 해결해보겠다.
  • 마지막 5천 회 반복 동안 모델 예측을 사용하여 $y_t$를 구성.
    • 코드와 로그를 확인해보니 160k iter을 일반적인 방법으로 학습하고, 가장 best 성능을 내는 weight를 가져와 재학습
  • 모델의 자체 예측에서 추가된 노이즈를 제거하도록 목표 변경.
  • 이로 인해 훈련과 테스트 간의 데이터 분포를 일치시킴
  • figure 3a를 보면 이 방식은 성능 저하대신 saturation 된 것을 확인할 수 있음

    

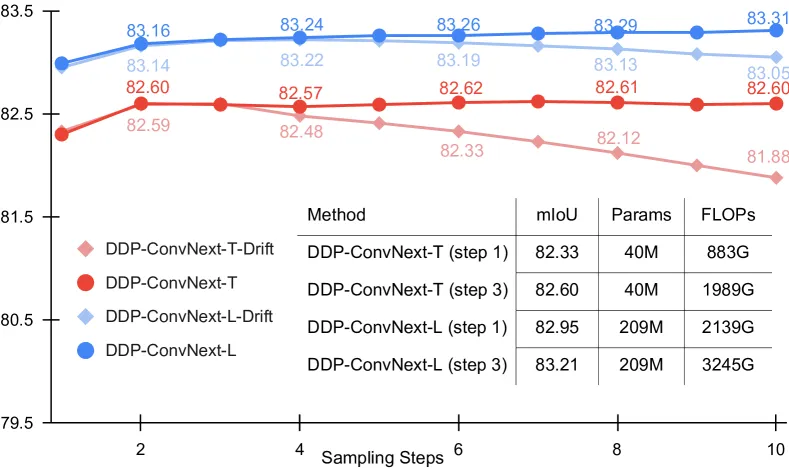
    Figure 3a

    
    
  • cityscapes 에 대해서만 진행한 듯
  • 이미지 생성작업에 비해 diffusion model을 perception task에 통합하면 효율성이 향상(생성은 DDIM 50 steps이 필요함) → 3 steps에서 만족스러운 결과 도출
  • 근데 config 파일을 확인해보면 self-denoising 때는 timesteps가 10임….

• Multiple Inference:
  • 여러 단계 샘플링 절차 덕분에, 컴퓨팅과 예측 품질 간의 트레이드 오프 지원.
  • 모델 예측의 신뢰성 및 불확실성 평가 가능.

Experiments

1. Main Properties

• 매력적인 특성
  • DDP는 다단계 샘플링 과정을 통해 연산 비용과 예측 품질을 자유롭게 조절할 수 있는 유연성을 가짐.
  • 확률적 샘플링 과정을 통해 예측 불확실성의 평가가 가능함.
• 성능 평가
  • Semantic Segmentation: ConvNext-T와 ConvNext-L 백본을 사용하여 샘플링 단계를 1에서 10까지 증가시켜 평가함. 예를 들어, ConvNext-T 사용시 단일 단계에서 82.33 mIoU를, 3단계에서는 82.60 mIoU를 기록함.
  • BEV Map Segmentation: nuScenes 데이터셋에서 실험을 수행하며, 주행 가능한 공간, 보행자 횡단보도 등 6가지 배경 클래스를 평가.
  • Monocular Depth Estimation: KITTI 데이터셋 사용. DDP는 특히 단안 깊이 추정에서 주목할 만한 데이터를 기록.
• 구성 요소에 대한 연구
  • DDP의 구성 요소들에 대한 세부적인 설명과 실험 결과는 부록 B와 C에서 제공됨.
• Dynamic Inference (동적 추론)
  • DDP는 여러 샘플링 단계를 사용하여 성능을 지속적으로 개선할 수 있음
  • ConvNext-T 백본을 사용하면 1단계에서 82.33 mIoU에서 3단계에서 82.60 mIoU로 증가
  • 이는 정확도와 계산 비용 간의 균형을 맞출 수 있는 유연성을 제공
  • 다양한 시나리오에서 네트워크를 재훈련할 필요 없이 속도와 정확도 간의 트레이드오프를 조정 가능
  • 그림 3a를 통해 여러 샘플링 단계에서의 성능 변화를 시각화할 수 있음
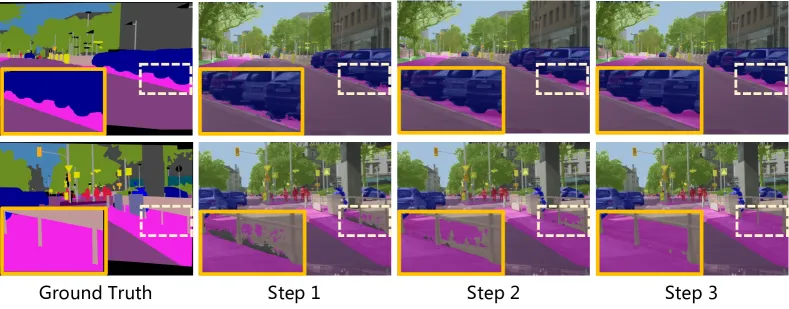
• Uncertainty Awareness: DDP(디퓨전 모델)는 특정 픽셀에서 예측 결과가 시간이 지남에 따라 어떻게 변화하는지를 추적함으로써 불확실성을 평가할 수 있음.
  • 변화 추적: 여러 단계의 샘플링 과정 동안 각 단계의 예측 결과가 이전 단계와 얼마나 다른지를 카운트함.
  • Normalization: 이 변화 카운트 맵을 0-1로 정규화하여 최종적으로 불확실성 맵을 얻음.
  • Uncertainty Map:
    • 높은 응답 영역: Uncertainty에서 높은 응답 영역은 높은 불확실성을 나타냄.
    • error map과의 상관관계: 불확실성 맵의 높은 응답 영역은 error map에서 잘못 분류된 픽셀(흰색 영역)과 높은 양의 상관관계를 가짐.
• 시각화: 더 나은 시각화를 위해 이미지를 확대하여 불확실성과 오류 간의 관계를 명확히 볼 수 있음.

2. Semantic Segmentation

• Dataset & Settings
  • ADE20K
  • Cityscapes
  • 512x512(ADE20K), 512x1024(Cityscapes)
• AdamW
• 160k iters
• ADE20K 데이터셋 결과:
  • DDP(단계 1)를 사용한 Swin-T 백본:
    • mIoU: 46.1
    • w/o diffusion process 대비 1.2포인트 향상 (46.1 vs. 44.9)
  • DDP(단계 3)로 성능 향상:
    • mIoU: 47.0
    • 추가 단계로 0.9포인트 증가
  • Swin-L 백본에서 최상의 성능:
    • mIoU: 53.2
    • UperNet 대비 1.1포인트 향상 (53.2 vs. 52.1)
  • 결론: DDP는 성능 향상과 유연성을 제공
• Cityscapes 데이터셋 결과:
  • ConvNeXt-L† 백본을 사용한 DDP(단계 1):
    • mIoU: 82.95
  • DDP(단계 3)로 성능 향상:
    • mIoU: 83.21
  • Swin-T 백본:
    • 단계 1에서 mIoU: 80.96
    • 단계 3에서 mIoU: 81.24
  • 다양한 모델 구조에서 DDP의 확장성 입증
  • 종합 결론: 멀티 스텝 디노이징 확산을 통해 성능 점진적 향상 및 비슷한 계산 오버헤드 유지
• DDP의 원래 목적:
  • 다양한 dense prediction 작업을 위한 일반적인 프레임워크 설계
  • Diffusion 기반 접근법 사용
• 현 상황:
  • DDP의 세그멘테이션 성능이 Mask2Former보다 약간 낮음(slightly lower)
  • 여전히 높은 경쟁력(highly competitive)을 갖추고 있으며 여러 매력적인 특징을 가짐
• 향후 과제:
  • 특정 세그멘테이션 작업에 최적화된 diffusion 프레임워크 설계
  • Mask2Former보다 더 나은 성능을 달성하는 방법 탐구 필요

5. Ablation

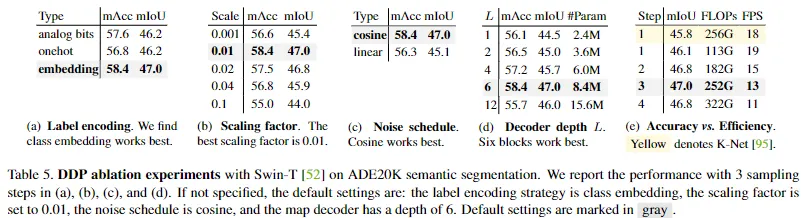
• 실험 배경:
  • 모델: Swin-T 백본 사용
  • 총 훈련 횟수: 160k iteration
  • 실험 설정: Section 4.2와 동일 (sem seg)
• Label Encoding (라벨 인코딩):
  • 이유: Semantic segmentation의 라벨은 이산적(discrete)이기 때문에 인코딩 필요
  • 테스트한 전략들:
    • One-Hot
    • Analog Bits
    • Class Embedding: 최적의 성능
• Signal Scale (신호 스케일):
  • 이유: Class embedding 전략에서 최적의 scaling factor를 찾기 위해
  • 결과: scaling factor가 0.01일 때 최고의 성능. 더 큰 scaling factor는 성능 저하를 초래
  • One-hot과 Analog bits에서는 0.1일때 가장 best
• Noise Schedule (노이즈 스케줄)
  • 비교: Cosine Schedule와 Linear Schedule을 비교.
  • 결과: Cosine Schedule이 더 나은 성능을 보임 (47.0 mIoU vs. 45.1 mIoU).
  • 이유: Cosine Schedule은 현실적인 점진적 신호 감소 시나리오를 시뮬레이션하여 모델의 노이즈 제거 능력을 강화함.
• Decoder Depth (디코더 깊이)
  • 비교: 디코더의 깊이를 비교.
  • 결과: 적절한 깊이가 필요함. 깊이가 증가하면 성능이 향상되지만, 과도한 깊이는 성능 저하를 초래.
  • 최적값: 6 블록으로 설정, 이는 8.4M 파라미터로 경량화됨. 대표적 method K-Net (41.5M), UperNet (31.5M)와 비교하여 효율적임.
• Accuracy vs. Efficiency (정확도 vs. 효율성)
  • 비교: DDP와 대표적 discriminative method인 K-Net를 비교.
  • 결과: DDP는 샘플링 스텝이 하나일 때에도 K-Net과 비교했을 때 더 나은 mIoU를 보이며, FLOPs가 적고 FPS가 높음.
  • 향상: 세 번 샘플링으로 성능이 47.0 mIoU로 향상되지만, 여전히 적정한 FLOPs와 FPS를 유지.

Conclusion

• DDP(Conditional Diffusion Model)의 도입
  • 간단하고 효율적이면서도 강력한 프레임워크로, conditional diffusion을 기반으로 한 dense prediction을 수행.
• 기존 방법론과의 비교
  • Architectural customization나 task-specific design 없이 modern perception piplines에 diffusion process를 확장
  • 다양한 작업 및 벤치마크에 대해 SOTA 또는 competitive 성능을 보여줌
  • 여러 번의 추론 및 불확실성 인식 기능을 가지며 이는 이전의 단일 단계 분류 방법과 대조됨
• 주요 장점
  • 세 가지 대표적인 작업과 여섯 가지 다양한 벤치마크에서 큰 성과를 보여줌
    • Cityscapes(83.9 mIoU), nuScenes(70.6 mIoU), KITTI(0.05 REL) 등
• 잠재적 단점
  • 여러 단계의 추론을 수행하기 때문에 추가적인 계산 비용이 발생할 수 있음
  • 다른 도메인에서도 동일한 효과를 보이는지에 대한 추가 연구가 필요

Appendix

A. Diffusion Model

• A.1. 알고리즘 세부 사항
  • Algorithm 1, Algorithm 2 보충
    • 논문 본문에 설명된 알고리즘 1과 2를 보완하기 위해 Algorithm 3의 구현 세부 사항을 제공.
  • Algorithm 4: Self-aligned 디노이징
    • 샘플링 드리프트 문제를 해결하기 위해 마지막 5K 반복 훈련에서 사용됨.
    • Figure 4는 훈련과 추론 denoising target간의 차이를 설명함.
• A.2. 추가 논의
  • 디퓨전 모델 포화점
    • "Figure 3a"에 설명된 것처럼, 지각 작업에 대한 디퓨전 모델은 첫 몇 단계 내에 포화점에 도달하는 경향이 있음. 일반적으로 3-5단계.
  • 생성 모델과의 비교
    • 이미지 생성 같은 생성 작업에서는 여러 단계(10 ~ 50 단계)에 걸쳐 점진적으로 더 높은 품질의 결과를 생성함.
    • 생성 작업: 여러 정보가 축적되어야 하므로 많은 단계가 필요지각 작업: 중요한 정보는 몇 단계 내에 축적되기 때문에 추가 디퓨전은 예측 정확도를 크게 향상시키지 않음.
  • 지각 작업의 디퓨전 프로세스
    • 이미지에서 라벨로 가는 과정은 정보 감소의 점진적 과정임. ⇒ 결정을 내리는데 필요한 중요한 정보를 몇 단계 내에 얻어야함
    • 따라서 추가적인 diffusion은 예측의 정확성을 향상시키는데 제한된 역할을
    • 중요한 정보를 빠르게 축적하여 의사결정을 할 수 있음.

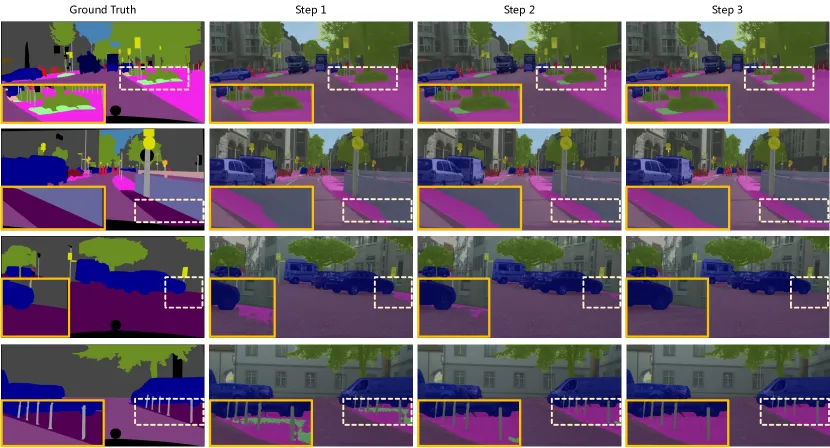
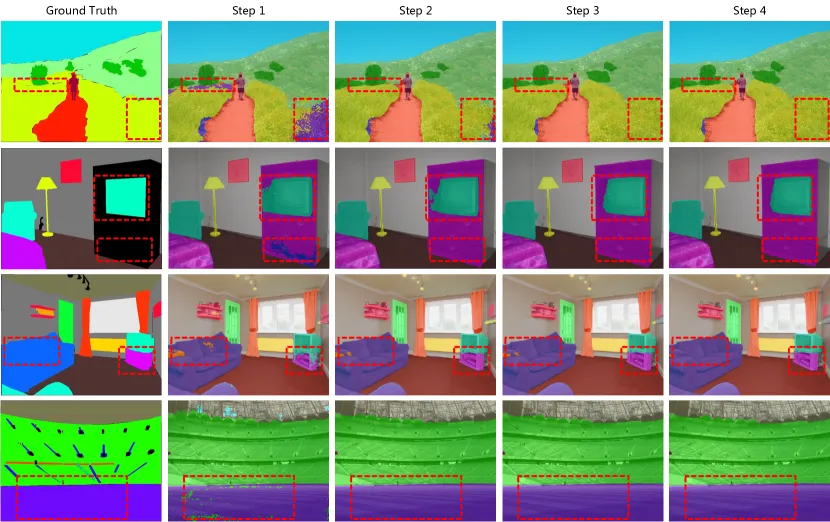
• Figure 5와 Figure 6: Cityscapes와 ADE20K 검증 세트에서 DDP의 "multiple inference" 속성을 시각화.
  • 이 속성은 DDP가 샘플링 단계를 더 많이 사용함으로써 성능을 지속적으로 향상시키고 더 부드러운 세분화 지도를 생성할 수 있음을 보여줌.

•